Enroll in The Flexibility Formula
Video with the CGI Math Stages (at around 5:46 into the video)
Welcome fellow Recovering Traditionalists to Episode 220 – The Math Fluency Trap: Why Flexibility Isn’t Enough
If you’re a math coach, you’ve probably found yourself caught in the middle of the fluency debate.
On one side, you’ve got people saying, “Kids need to memorize their facts. We need more drill and practice.”
On the other side, you’ve got people saying, “Timed tests create anxiety. We should never drill facts.”
And you’re stuck in the middle thinking, “There has to be a better way.”
Well, there is.
Today, I want to talk about that fluency trap—speed is important but it isn’t enough, flexibility is important, but it isn’t enough either. So stick around to learn what math fluency actually entails and how we can help our teachers get out of this all-or-nothing thinking.
True math fluency has three components: Accuracy, Efficiency, and Flexibility.
Accuracy – getting the right answer. Yes, that matters. We’re not throwing that out.
Efficiency – being able to get to the answer in a reasonable amount of time. Not necessarily 1 second, but not 5 minutes either.
But here’s the piece that’s almost always missing: Flexibility.
Flexibility means having multiple strategies to solve a problem. It means understanding relationships between numbers. It means if you don’t immediately know 8 + 7, you can think, “Well, 8 + 8 is 16, so 8 + 7 must be one less—that’s 15.”
Flexibility leads into math fluency, but it isn’t the only thing your students need.
I am a huge proponent of building number flexibility in students. I have classes called The Flexibility Formula. Yet we have swung the pendulum to ONLY focusing on Flexibility and that’s not good for students.
For years the way we taught math fluency was through worksheets, drills, and timed tests. That had some major downsides to it so the pendulum swung away from that and I’ve seen (and heard from others) that helping build students’ flexibility isn’t working and that’s because the pendulum needs to stop in the middle.
When kids have flexibility with numbers—when they see relationships and can use strategies—they can figure out problems without shutting down; however for facts to eventually become automatic students do need repetition and practice. Fluency isn’t just Flexibility and it isn’t just Efficiency. Students need all 3: Accuracy, Efficiency, and Flexibility.
I get it, teachers are hearing, “Don’t do timed tests. They create anxiety.”
But in the day-to-day reality of working with students they see their students struggling to solve problems because they’re still counting on their fingers for basic facts.
And they think, “Well, if I’m not supposed to drill facts, how are they ever going to learn them?”
So they either go back to drill and practice (because at least that’s something), or they avoid practice altogether (and hope fluency magically happens).
Neither works.
Instead, there’s a third option: Purposeful practice that builds flexibility.
Let’s take a look at 3 ways I like to help teachers along their way to doing that and 3 people I’m excited for you to learn from at the upcoming Virtual Math Summit.
FOCUS #1: THE FOUNDATIONS OF FLUENCY
The first thing I’d recommend you do is make sure you’re all on the same page about what fluency actually means at your school.
Because if teachers think fluency equals speed, they’re going to keep drilling facts and timing kids.
So introduce the three components: Accuracy, Efficiency, and Flexibility.
And then give them an example to make it concrete:
Think about a student who knows 8 + 7 = 15 because they memorized it. That’s accuracy and efficiency. Great.
But what happens when they see 18 + 27? If all they have is memorization, they’re stuck with only stacking the numbers and doing the algorithm.
But if they have flexibility—if they understand that 18 + 27 is like how they think about 8 + 7 and they see they can do 18 + 2 to make 20, and now you have 20 + 25 —they can quickly create easier problems from ones they don’t know. And often that is faster than doing the algorithm.
That’s the power of flexibility.
Once teachers understand that flexibility is the missing piece, they start asking different questions.
Instead of “How do I get them to memorize (or do the algorithm) faster?” they start asking “How do I help them see relationships between numbers?”
And that’s when the real work can begin. If you want help with this part of building fluency, check out The Flexibility Formula courses we have for math coaches and elementary teachers to build your understanding of Fluency, what it entails and how to help students build their Flexibility on their way to Math Fluency. You can find out more about the courses at BuildMathMinds.com/enroll
FOCUS #2: PURPOSEFUL PRACTICE STRUCTURES
The second thing I’d focus on is showing teachers that there’s a middle ground between drill and practice and just letting kids play around with quantities.
It’s purposeful practice—practice that builds flexibility and efficiency, not just memorization.
And there are so many ways we can do that but here are a few of my favorites.
Number strings are one of my favorites. You use a string of problems that are connected—like 8 + 8, then 8 + 7, then 6 + 6, then 6 + 5, then 9 + 9, then 9 + 8. You’re doing a series of problems but they are related in some way to practice but also reinforce that flexibility.
Strategy-based practice is another one. Instead of giving students a worksheet with 50 problems to solve as fast as they can, give them 10 problems that are related in some way…or even give them the worksheet of 50 problems BUT they have to go through and find 10 problems that they would solve using the same strategy and then solve them, showing the strategy they used not just the answer.
This forces students to think flexibly instead of just racing to get answers.
And games—games are such a powerful way to practice facts in a low-pressure, engaging way. But the key is giving students choice in how they solve problems while they are playing.
The goal isn’t for everyone to use the same strategy. The goal is for everyone to have a strategy that works for them.
Now, I know what you’re thinking. Teachers are going to push back on this.
“But they need to practice more than 10 problems.”
And yeah, they will in some of the activities. But in the beginning, we’re building flexibility. Too many problems seems overwhelming to students who are still developing strategies. Once they have flexibility, we can increase the volume of practice. But if we move too quickly to tons of problems, we end up just reinforcing inefficient strategies because the kids want to ‘just get this done with’.
FOCUS #3: THE PROGRESSION OF FLUENCY
The third thing I focus on is helping teachers understand that fluency doesn’t happen overnight. It’s a progression.
And different students are going to be at different places in that progression.
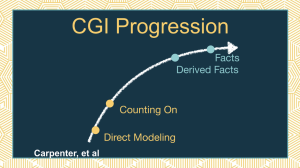
If you’ve been around for awhile this Cognitively Guided Instruction progression should be familiar, if you haven’t I’ll link to other trainings where I go deeper into that. But I wanted to remind you kids start out at the direct modeling stage, move into counting, then derived facts, and facts.
But here’s the key: You can’t skip stages.
If a student is in Stage 1 (counting everything), we can’t just tell them to memorize facts and expect them to jump to Stage 4. Well I mean you COULD do that but this is where we see kids who have some memorized but then fall back to needing manipulatives or their fingers to figure out a lot of the problems.
They need to move through Stage 2 (counting) and Stage 3 (using strategies) if we want to develop true fluency.
And Stage 3—using strategies—is where flexibility is built. That’s the stage we absolutely cannot skip.
So when a teacher is frustrated because their students are still counting on their fingers, help them see that counting on fingers is actually progress. It means they’ve moved from Stage 1 to Stage 2.
Our job now is to help them move into Stage 3—where they’re using strategies and seeing relationships. And then start practicing more to make those strategies more automatic.
Yet again, this is the stuff I help you with inside The Flexibility Formula courses. But this video really wasn’t supposed to be about my courses. It’s about seeing what other experts have to say on the topic of fluency as well and we’ve got some great ones joining us for the 2026 Virtual Math Summit at the end of February.
First, Pam Harris is doing a keynote called “Five Most Important Teacher Moves.” Pam is one of the biggest names in math education, and she’s all about helping students become flexible thinkers. Her five teacher moves are practical, research-based, and will give you a clear roadmap for building real fluency—not just speed. I’m really excited about this one.
Second, Dan Finkel is doing a session for math coaches called “Purposeful Fluency: Using Choice and Structure to Make Practice Meaningful.” This is exactly what we’ve been talking about today—how to give students practice that builds flexibility, not just memorization. Dan’s going to show you how to make practice engaging and effective. If you’re struggling with the “how do I practice facts without drill and practice” question, this session is the answer.
And third, Becky Lord is doing a session called “How the Neuroscience of Math and Dyscalculia Can Transform Number Sense and Math Fact Fluency for ALL.” This is the WHY behind everything we’ve talked about. Becky’s going to dive into how brains actually learn math facts. When you understand the neuroscience, you can explain to teachers why building flexibility matters. And that’s powerful.
All three of these sessions will give you the tools, the language, and the confidence to help your teachers stop the pendulum swing and get out of the fluency trap.
And they’re completely free.
Go to VirtualMathSummit.com and get registered. The summit starts February 28th, and there are over 34 sessions for elementary math coaches and teachers.
Fluency isn’t about speed. It’s about accuracy, efficiency, and flexibility.
And flexibility is often the missing piece, but it isn’t the ONLY piece we need to develop.
When we help our teachers understand the 3 parts to fluency, introduce purposeful practice structures, and show them the progression, we help them get out of the fluency trap.
And we help their students build real, lasting fluency.
Alright, my fellow Recovering Traditionalists, I hope this helped build your math mind so you can build the math minds of students.




