Welcome fellow Recovering Traditionalists to Episode 213: Seeing Multiplication – How Subitizing Builds Fact Fluency Through Relationships
Have you ever watched a student count out 6 items 4 times, to get the answer to 4 x 6? And then five minutes later need to count all over again for the exact same problem? What if instead, that student could instantly “see” that 4 times 6 is just double 2 times 6, without counting at all?
In this episode, we’re exploring how subitizing—that ability to instantly recognize quantities without counting—completely transforms multiplication from 100 isolated facts to memorize into a beautiful web of connected relationships that students actually understand.
What Is Subitizing & Why It Matters
If you’ve been listening for a while, you know that subitizing is one of the eight foundational number sense concepts. It’s that instant recognition of quantity—like when you roll dice and immediately know you got a five without counting the dots.
When we apply this to multiplication, we are encouraging kids to actually see the groupings and not individual items to be counted. We’re helping them instantly see equal groups and recognize their structure. This is the leap from additive thinking—where everything is about counting on—to multiplicative thinking, where students see relationships and patterns.
The Problem with Traditional Multiplication Teaching
Without these relationships, we get caught on the “times tables treadmill.” This is where we teach kids their ones, then their twos, then their threes, marching through each set of facts in isolation and cycling back to each ‘set of facts’ to ensure they have been memorized.
Here’s the problem: this approach creates 100 separate, unconnected facts for students to memorize. And what does research tell us about isolated memorization? Researchers have shown repeatedly that when students learn math as disconnected facts rather than as relationships, they forget quickly. They’re trying to hold 100 separate pieces of information in their heads instead of understanding key facts and the relationships that connect everything together.
Without a visual and conceptual foundation, students miss the absolutely beautiful patterns in multiplication. They don’t see that every fact connects to other facts. They’re so busy trying to remember “what’s 7 times 8” that they never realize it’s just one less group of 8 than 8 times 8, or two more groups of 8 than 5 times 8.
Building Multiplication Through Strategic Fact Families
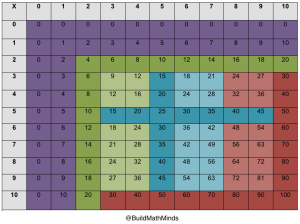
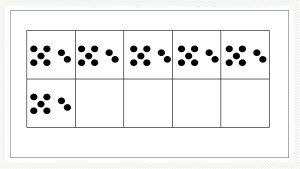
So here’s how we flip the script. Instead of marching through the times tables, we start with the 4 Types of Multiplication Facts: times 2, times 10, times 5, and x0/x1 (properties of multiplication). For those watching the video, you see my multiplication chart right now—and I’ll make sure there’s a link in the show notes for those listening—these facts create the backbone that everything else connects to.
Let’s start with times 2—our doubles. This is where you can ensure your students are able to subitize the small amounts, because later we are going to have a lot more groups of these so we need to ensure kids can subitize one or two groups first. PLUS, I love starting with times 2 because it is their doubles addition facts which they’ve been working on for a few years. Doubles are typically the first multiplication facts children naturally acquire because they’re so easy to visualize and so common in their world. So, try this in your classroom tomorrow: make dot cards showing two groups of 3, two groups of 4, two groups of 6. Flash them for just 2 or 3 seconds. Students with developed subitizing don’t count—they just see “two groups of 4, that’s 8.”

Next, I like to develop times 10. We often teach the trick to just “add a zero” when multiplying by 10 but if you’ve ever worked with middle school kids, that trick stops working when multiplying with decimals. Instead we need kids to understand that the number gets 10 times bigger and that moves it over into a new place value…it’s not just adding a zero. Instead, let’s make it visual. When students have been working with ten frames since kindergarten, seeing groups of 10 is automatic when we put groups of dot patterns into the ten frame. In this visual I’m showing groups of 4, but you can’t tell how many groups there are because they are just randomly placed.

When I put them into this ten frame you can subitize and know there are groups of 4 but you also know there are 10 groups because the ten frame is full.

At this point you might have students who can tell you there are 10 groups of 4, but then they have to count every single dot to determine who many total dots. And that’s okay, that’s where many students will start out. But at least now they weren’t counting out every single one of those groups and counting to ensure there were 10 groups. Multiplication is a WHOLE LOT OF COUNTING unless your students can subitize. I believe that’s one of the main reasons we jump to just memorizing the facts because counting is so time consuming and we don’t know what to do instead of that to help them. Subitizing is the key.
So after times 10, I like to work on times 5 facts. Fives are easy for kids to count by, but also you can connect how having 5 groups of something relates to having 10 groups of something.

And because 5 and 10 are those Benchmark numbers once they have 2, 10, and 5 they can figure out all the other facts.
The last Type of Fact, is Times 0 and Times 1…these are properties of multiplication but they are hard for kids to wrap their brains around right off the bat when they are trying to understand multiplication. So I like to wait on these until they get a sense of what multiplication means through their work on developing x2, x10, and x5.
Now here’s where it gets really interesting. Once students own these 4 Types of Facts, everything else is just one step away. Times 4 facts? That’s just double-times 2. Show students 4 times 6 as dots. They see 2 groups of 6—that’s 12—then double it to 24. They’re subitizing at each step, not calculating.
Times 3 facts? That’s just one more group than times 2. When I show 3 times 7 with dots, students who can subitize see “Oh, 2 sevens is 14, so 3 sevens is just 7 more—21.” They’re using what Carpenter, et al called Derived Facts through their work of Cognitively Guided Instruction—building unknown facts from known facts through relationships.
From Equal Groups to Arrays
Let’s talk about the visual progression because we can’t stay with ten frames forever. Kids naturally start with scattered equal groups using non-subitizable amounts. Picture 3 groups of 4 dots, scattered on the page. We need to help them organize those so they are subitizable. That’s why I love ten frames. As your students are counting out their groups you can have them put their groups into a big ten frame on their desk. You can encourage them to make the groups inside each spot subitizable also…just take a minute to ask them to look over at their shoulder partner’s ten frame and see if you can tell how many are in each frame.
After working in ten frames for a while I do want you to move towards arrays. Because soon the amount in the groups is going to be large, too large to just subitize but we can help them subitize by changing up the colors.
If we have a 3 by 4 array, they can still see the 3 and 4…the rows and columns are subitizable.
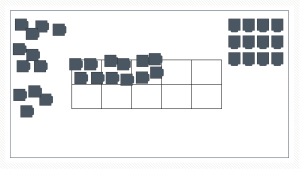
But if we have anything larger, kids will start to count again unless we help them see groups with coloring.
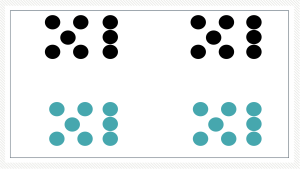
If your students have used rekenreks in the earlier grades they are familiar with the idea of colors changing once there is 5 of something. You can also do this with connecting cubes. Once there’s 5, I will switch the color of the counters. Then when we line those up in an array format, it is now subitizable.
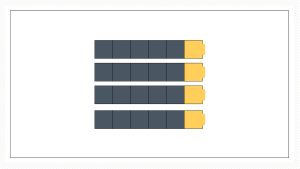
The array/area model is really essential to help students understand the commutative property. When students can mentally rotate and reorganize quantities, they understand that 3 groups of 4 and 4 groups of 3 are the same because they can see it, not just because someone told them about the commutative property. That’s easier to see with array/area models and harder to do when the only visual they have are equal groups.
Classroom Strategies
Alright, let’s get practical. Here are three strategies you can start using tomorrow.
First, Quick Image warm-ups. Flash arrays on your screen for just 2 to 3 seconds. Start with those 4 Types of Facts—times 2, 5, 10, and 0/1. After the image disappears, students describe what they saw and how they knew. “I saw 3 groups of 5. I knew it was 15 because I saw the 10 and then 5 more.” Then connect that to the abstract by creating the equations. You’re building both subitizing and multiplication reasoning.
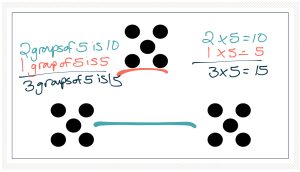
Second, encourage your students to see connections by doing activities like “Build It From What You Know.” An example is to show students 6 times 7 visually. Don’t let them calculate from scratch. Ask: “What do you see in this visual that could help you?” Some students might see it as 5 times 7 plus one more 7. Others might see it as 6 times 5 plus 6 times 2. The key is they’re seeing the relationship, not counting from zero.
Third, use color-coding with visuals that aren’t easily subitizable. When you’re working on 4 times 8, explicitly connect it to doubling by changing out the colors in each of the 2 groups of 8. Discuss it as a class to make these connections visible and explicit every single time.
Connecting Back to Number Sense
If you didn’t notice it throughout our discussion here, I want to explicitly point it out. The 8 number sense concepts layer together to help your students build their understanding of multiplication. I didn’t talk about it in this video but the three counting concepts are where your students start in their development. But then we layer in Subitizing to help them get past counting. By using subitizable images you help your students see Spatial Relationships. Part-part-whole thinking allows students to see 7 times 6 as 5 times 6 plus 2 times 6. They’re decomposing based on friendly numbers (aka Benchmark Numbers), not following a rule.
The concept of One or Two More or Less? Did you notice that when students use that strategy of 7 times 6 is just two more groups of 6 than 5 times 6?
All 8 of the number concepts play a role in helping your students develop their understanding of multiplication and so much more. If you want to learn more about the 8 concepts and how they help develop your students’ understanding of mathematics, check out my online course for teachers: The Flexibility Formula. The Flexibility Formula 3rd-5th grade specifically builds your understanding of the 8 concepts and how to help your students go from mindlessly following procedures to thinking flexibly when solving problems. Go to BuildMathMinds.com/enroll to learn more.
Next Steps
Whether or not you do the online course, please start using subitizing to help your students understand multiplication. That way you are not asking students to memorize 100 facts. You’re helping them develop the 4 Types of Facts and the key relationships that connect everything together. They understand that 8 times 7 is related to 8 times 5, and 10 times 7, and even 4 times 7. It’s all connected.
Your challenge for tomorrow: Pick one multiplication fact that your students struggle with. Let’s say it’s 7 times 6. Instead of practicing it in isolation, help them see its connections to something they do know. Show them how it relates to 5 times 6, or 7 times 5, or double 7 times 3. Use visual models. Use subitizing. Build the relationships.
And teachers, I have that color-coded multiplication chart available for you—check the show notes at buildmathminds.com. It’s designed to help you and your students see these connections visually.
Remember, we’re not building calculators here. We’re building mathematical thinkers who see the patterns, understand the relationships, and find beauty in the structure of numbers. When multiplication becomes about relationships instead of memorization, everything changes.
Alright my Fellow Recovering Traditionalists, I hope this helped build your math mind, so you can build the math minds of your students.




