Resources mentioned in this episode:
Welcome fellow Recovering Traditionalists to Episode 130. Today I’d like to talk about Building our Understanding with Dr. Ange Rogers, Duane Habecker, and Shannon McCartney.
The Flexibility Formula is an online PD course I have, but it’s also a framework we can use to help us build math minds and not just create calculators. There are 5 pillars to The Flexibility Formula: Equity & Access, Understanding, Observing, Connecting, and Experiencing.
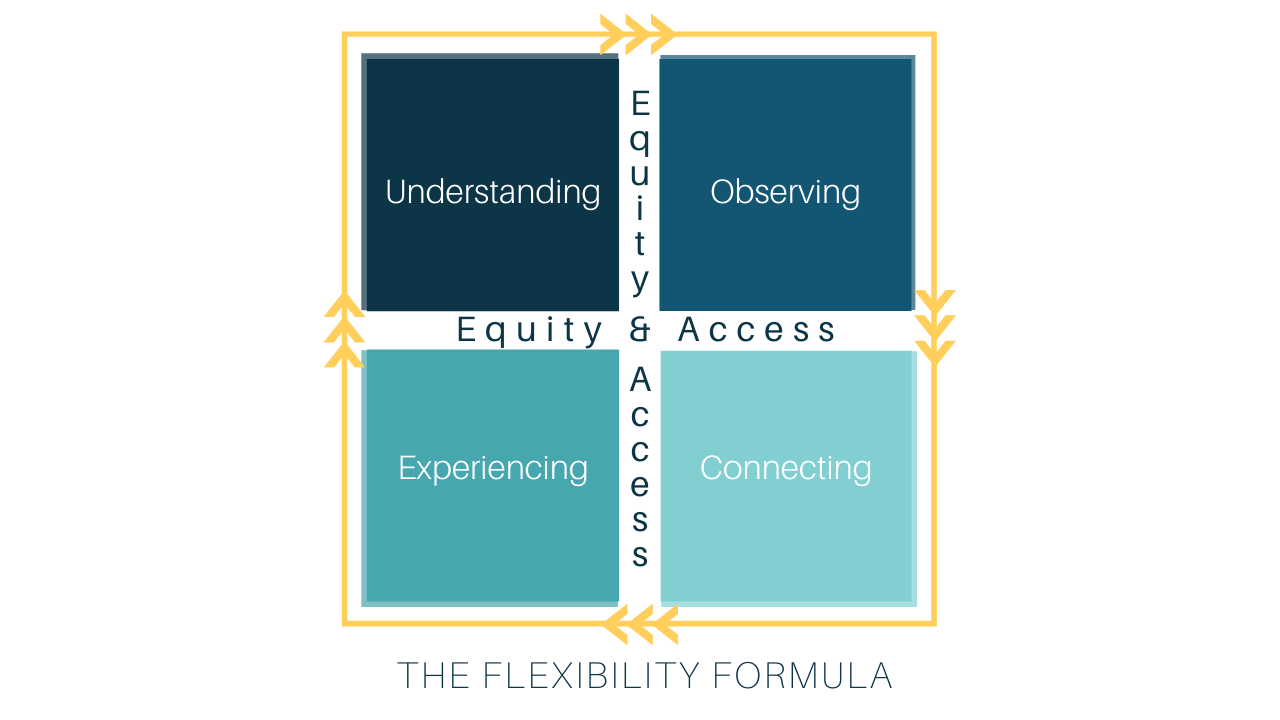
All of the sessions at the 2022 Virtual Math Summit address one or more of these pillars. So for the next few podcast episodes leading up to the summit on February 26 & 27, I’m going to share a few sessions that address each of the 5 pillars. In this episode we are going to look at the Understanding pillar and how presenters Dr. Ange Rogers, Duane Habecker, and Shannon McCartney address the pillar in their sessions.
Understanding is about building our understanding of the math so that we can help our students build theirs. If you are like me, I learned the procedures & steps of doing math but I didn’t actually understand it and how it all works together and I was horrible at applying the steps to real life situations and problems. Kids need to develop Procedural Fluency, but they also need Conceptual Understanding and Application.
Up first in the podcast we are going to take a listen to Dr. Ange Rogers. In her 2022 Virtual Math Summit sessions she is sharing information about place value. She has a mini-session about a place value assessment, but her full session is all about building our understanding of place value and how we can build it for the kids. In this sneak peek she is sharing how to help kids understand the patterns that are in our number system to help kids learn how to read large numbers.
Dr. Ange Rogers: “And so I go on to show them this template that will help them to be able to read numbers just as large as that one. So we talk about place value houses. And so the official name is periods. So each of these houses is a period. So we’ve got the billions period, the millions period, the thousands period, this one over here is the ones period. And so in each of the periods, we have hundreds, tens and ones. So in the thousands period, we’ve got hundreds of thousands, tens of thousands and thousands. In the millions period we’ve got hundreds of millions, tens of millions and millions. And in the billions period, the same, hundreds of billions, tens of billions and billions. So really all children need to be able to do to read a large number is to read a three digit number and then name the period that that number is in.
So here we’ve got 301 million we say, because it’s in the millions period. 107 thousand and then the ones house we call them the trend setter because they started the pattern. So you don’t actually have to say their name. So you just say 201. So this number (301,107,201) would be 301 million 107 thousand 201. So you can see that this structure really makes the pattern clear, the structure clear for them.
So we want them to be investigating our number system and making sense of it. They love working with big numbers, so don’t be afraid of letting them do that. They show a pattern of our number system. So we want them to be investigating the names of their periods like trillions, quadrillions, quintillions, et cetera. We also want them to know amazing facts, like a number with a hundred zeros is called a googol.
Some teaching tips around this. So once students can read a three digit number, they’re ready to move on to reading large numbers. So if you think of reading, we don’t say, ‘Okay, we’re going to teach you to read a three letter word and then a four letter word, and then a five letter word.’ We teach it in more of a pattern or a structured way. And so that’s the same, we want to do that in reading numbers as well. We want them to see that there is a pattern that they can apply across the number system. So we don’t need to teach them three digit numbers and then four digit numbers and then five digit. Once they can read a three digit number, we should be teaching them how to read numbers of any magnitude.”
Up next is Duane Habecker. Duane has done sessions for past Virtual Math Summits and I’m so excited to have him back again this year. In his session he is showing us how to use dots to help kids understand the traditional algorithms for all 4 operations: Addition, Subtraction, Multiplication, and Division. In this sneak peek of his session he is sharing the difference between a strategy and an algorithm and how they work together to build students’ understandings.
Duane: “In order to really dig into what we mean by algorithms, first I want to talk about what this means in relation to strategy. So strategies versus algorithms. Because I want to be clear and make sure we’re all on the same page. They’re not exactly the same thing. We need them both. But they’re not the exact same thing. I’m going to focus in this talk on algorithms. But strategies, so a strategy are computations that the students come up with generally on their own based on number sense and sense making. They use their understanding of numbers in a variety of different ways to arrive at an answer. And oftentimes, these strategies are not exactly generalizable. So that’s a strategy. Oftentimes, student-invented based on number sense, not always generalizable.
An algorithm, on the other hand, is this idea of decomposing numbers generally using the base 10 notation, so that this collection or this big operation is really now decomposed into a series of single digit computations. And this algorithm is generalizable. All right.
Now the important thing is I’m not saying one versus the other. We need them both, but we have to acknowledge that strategies are not algorithms. Strategies are, however, incredibly, incredibly important.
Students who used invented strategies before learning that standard algorithm, they do better in terms of demonstrating place value and properties of operations than the students who just learn the algorithms right upfront. All right. So these strategies are essential for developing a deeper understanding later with the algorithms. So we need them both.
But this talk is mostly going to focus on that algorithm portion of that two-step dance, I suppose. Now we know that visual math improves performance. And so I’m going to show you how to use these dots as a visual representation to help students make sense of those standard algorithms. Tons of evidence out there that says when we use visual representations to help students understand math, they do it better, they learn it better.”
Shannon McCartney’s session at the 2022 Virtual Math Summit is about using Place Value Strips to help kids build their understanding of lots of math standards throughout the elementary grades. What Shannon calls Place Value Strips, I have always called Place Value Cards and I know other people who call them Hide Zero Cards. They are number strips that can be placed on top of each other so kids see the actual numbers. So for the number 842, there is an 800 strip, a 40 strip, and then the 2 and when you stack them on top of each other it becomes 842. In this sneak peek, she is sharing how the strips can be used to help kids with rounding to the nearest 100. In her session, Shannon is showing a LOT of visuals which you can’t see on a podcast. Here is Shannon.
Shannon: “Let’s try this third grade strategy of rounding to the nearest hundred using place value strips.
I have the number 842, we want to be able to round this to the nearest hundred. Oftentimes when we’re rounding to the nearest hundred, or even by 10, it’s really great for kids to have a visual at the place value strips of a number line. So I’m going to go ahead and create a number line here, and I’m going to start my number line at the value of what we’re looking at, which is 800. I’m trying to decide if 842 is closer to 800 or our next hundred up, which is going to be 900.
The next question we want to ask kids once they’ve created this number line is, ‘What is the halfway point or the midpoint?’
I don’t know about you but so many kids when I’m asking them, okay, ‘if I have 800 and 900 what’s halfway in between?’, they look at me like I’m crazy. So I use the abacus over and over and over again. The other day in a classroom a kid said, “Is it always going to be 50 Mrs. McCartney?” And I said, “Yes, because we’re talking about it within hundreds.”
Let’s check that out on the abacus. So if I was indeed looking to see is the midway point, so before I’m even thinking about plotting this 42 on here, what is half way? So a lot of students need to really think about the abacus technically has 100 beads on it, so I’m looking at this would be 800 and I’ve added all these beads, we’d be at 900.
So I tell kids, as they’re thinking about this, I’m going to start to count to see when I’m halfway. So, 810, 20, 830, 840, 850. Looking at the beads, we can see we’re at the halfway point. So halfway between 800 and 900 is 850. This will help them as they’re starting to plot this on their number line, so if we kind of go back to this number line here, we now can put in where that halfway point is, which is 850. So we’re looking at that number 842, kind of going along thinking if I were counting on this number line 800, the 10s, the 20s, the 30s, the 40s, wait a minute, we can see that 842 would be about here. Therefore, we haven’t hit that halfway point. We’re going to round this and keep it the same at the 800.
Now that we have that 800, if you want to, kids can go ahead and put in the red 10s and the white ones, the value of zero. So here, I’m going to go ahead and put in that we have zero 10s and zero ones to show that the number 842 rounding it to the nearest hundred was closer here to the 800.
I think using the place value strips is really valuable with the abacus, the place value strips and a number line to help kids to really understand and slow down the process. How is this different than ‘Underline the number. Is it five and higher, four and lower? Round up, keep it the same?’ A lot of kids learn a lot of tricks for rounding, there’s no tricks in math. Understanding it conceptual like this will help them understand it as they go on to doing this with decimals and estimating sums. So it’s really important to slow it down, use these tools to help kids to understand the why before the how.”
Now these are just 3 sessions that help us build our understanding so we can help our students build theirs, but many more of the 31 sessions do the same.
As always, I hope this has helped you build your math mind so you can build the math minds of your students.
This episode is brought to you by the Build Math Minds professional development site. It’s an online site full of PD videos designed specifically for elementary teachers to help you build your math mind so you can build the math minds of your students. If you are interested in getting in-depth Math PD at Your Fingertips, become a member of Build Math Minds. Just go to buildmathminds.com/bmm and depending upon when you are listening to this, enrollment might be open or you can join the waitlist and get notified when it opens again.




