Welcome fellow Recovering Traditionalists to Episode 212: Subitizing With Fractions
Subitizing has been heavily talked about for our young learners, but subitizing is so powerful for upper elementary kids for both fractions and multiplication. In this episode I’d like to explore what subitizing with fractions looks like.
So let me back up for a second. If you’re not familiar with subitizing, subitizing is the ability to instantly recognize how much without needing to count. So if I hold up three fingers, you don’t count one, two, three. Your brain just knows – that’s three. That’s subitizing. And we spend a ton of time in the early grades helping kids subitize small amounts with whole numbers.
Now, why does this matter for fractions? Well, think about what fractions actually are.
They are the repetition of a unit that is less than one. I know we talk about fractions as “part of a whole” but it’s really a limiting view of fractions for kids. The numerator is the count, or number of items. And the denominator is the denomination, or size of those items. So with ⅔ we want students to think of that as 2 one-third pieces. And one of the best ways to help them understand that is by developing the 4 Early Numeracy Concepts (which I’ve discussed in other videos that I’ll link in the show notes) with fractions. One of those early numeracy concepts is Subitizing.
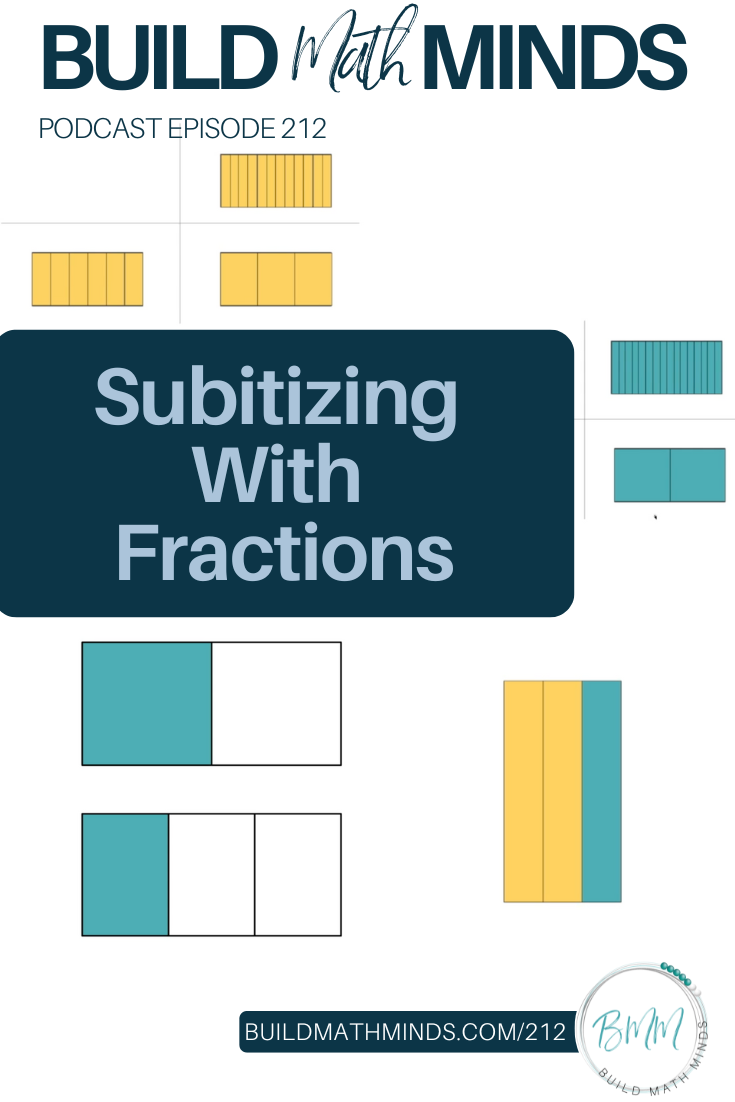
So what does subitizing with fractions look like. Well, first off it needs to be small numbers. Even as adults our ability to subitizing is around 3-5 unless it’s in some kind of pattern or grouped into those smaller amounts. When kids first recognize the dice pattern for 6, they don’t actually see it as 6 things. They see the 3 and 3. Then later they start to just recognize that pattern as a 6. When we are working with fractions the quantities we use for the numerator and denominator need to be small or else kids will count instead of subitizing.
If I show a rectangle divided into 8 equal parts with 6 of them shaded in, kids will not be able to subitize that. However, if the rectangle is cut into fourths and I shade in 3 of them, that is subitizable. Technically they are equivalent but one is subitizable and one is not.
Why is subitizing with fraction helpful? Well just like subitizing with whole numbers it helps children create visual representations of abstract quantities and when they have visuals they can compose and decompose the quantities as visuals easier than the symbols. And why does that matter? It really is the foundation of so many things.
But one example is they will actually understand what’s happening when they add/subtract/multiply/divide.
For instance when I show ¾ and ¾ together on the screen… if they can’t subitize, the students tend to count each piece to figure out it’s 6/4 and actually if they are counting they are more likely to say the image is showing 6/8. But students who subitize see the groups, they aren’t focused on individual pieces and so their strategies for adding tend to be grouping strategies. So you might hear a kids say something like, I saw that the first rectangle is just missing one-fourth so I took one from the other rectangle so that made it a whole and two-fourths left.
Another example is helping students understand equivalent fractions. Think back to when I said I wouldn’t use a visual of 6/8 for subitizing, well I actually would…but only if I’m using it alongside ¾ or actually under it. I would do a Quick Image flashing ¾ and ask the students what amount was shown. Then I’d flash two images at the same time and they have to tell me if the quantities are the same, or which one is showing a larger fractional amount. And in that next image I show ¾ towards the top of the screen and 6/8 underneath it.
I’m not expecting them to subitize the 6/8 but I am expecting them to see how it relates to the ¾ and use that relationship.
And that right there is the power of subitizing. It allows students to focus on relationships between quantities because they aren’t bogged down by counting. Now counting is important and yes even counting with fractions, but subitizing (the ability to tell how many without counting) is also very important for fraction sense development.
If you haven’t done much fraction subitizing, I’ve got a free download of Fraction Subitizing Cards.
If you want to delve even deeper into developing subitizing and all the number sense concepts check out The Flexibility Formula course. There is one specifically for 3rd-5th grade educators that builds your understanding of the 8 concepts and how to help your students go from mindlessly following procedures to thinking flexibly when solving problems. Go to BuildMathMinds.com/enroll to learn more.
Until next week my Fellow Recovering Traditionalists and I hope this has helped you build your math mind so you can go build the math minds of your students.
Subscribe and Review in iTunes
Other Ways to Listen To This Episode
Pin This To Pinterest for Later
